De Um Exemplo De Numero Racional E Um De Iracional – De Um Exemplo De Número Racional E Um De Irracional: A distinção entre números racionais e irracionais é fundamental na matemática. Compreender suas definições, representações e propriedades é crucial para o desenvolvimento de conceitos mais avançados. Esta análise explorará exemplos concretos de cada tipo numérico, contrastando suas características e demonstrando a riqueza e a complexidade do sistema numérico real.
Números racionais, expressáveis como frações de inteiros, possuem representações decimais finitas ou periódicas. Já os números irracionais, como π e √2, não podem ser expressos dessa forma, apresentando decimais infinitos e não periódicos. A compreensão dessa diferença é essencial para diversas áreas da matemática, desde a álgebra elementar até o cálculo e a análise matemática.
Números Racionais e Irracionais: De Um Exemplo De Numero Racional E Um De Iracional
Este artigo apresenta uma análise comparativa entre números racionais e irracionais, definindo-os formalmente, fornecendo exemplos e explorando suas propriedades e representações decimais. A compreensão dessas diferenças é fundamental para o desenvolvimento de conceitos matemáticos mais avançados.
Definição de Números Racionais e Irracionais
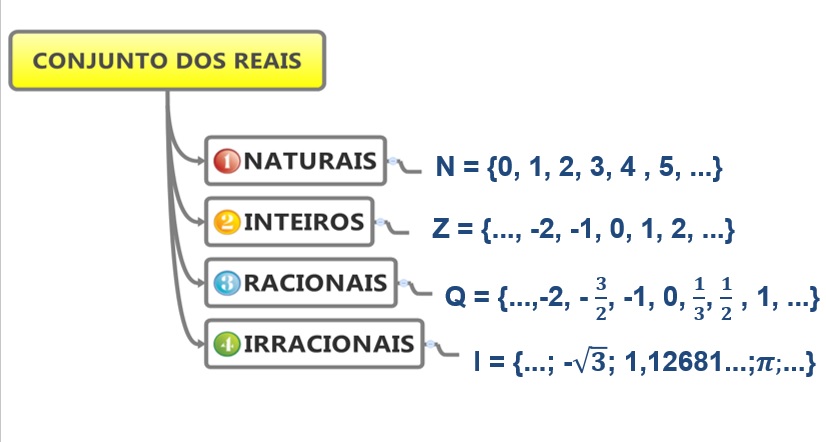
Números racionais e irracionais formam a base do sistema numérico real. A distinção entre eles reside na sua representação fracionária e nas características de suas expansões decimais.
| Tipo de Número | Definição | Exemplos | Propriedades |
|---|---|---|---|
| Racional | Qualquer número que pode ser expresso como uma fração p/q, onde p e q são inteiros e q ≠ 0. | 1/2, 0.75, -3, 22/7, 0 | Representação decimal finita ou periódica; fechamento sob adição, subtração, multiplicação e divisão (exceto por divisão por zero). |
| Irracional | Número que não pode ser expresso como uma fração de dois inteiros. | √2, π, e, √5 | Representação decimal infinita e não periódica; não fechamento sob adição, subtração, multiplicação e divisão com números irracionais. |
Exemplos de Números Racionais
Números racionais são abundantes e incluem inteiros, frações e decimais finitos ou periódicos. A conversão entre frações e decimais é um processo direto.
Exemplos de números racionais positivos:
- 1/2 = 0.5
- 3/4 = 0.75
- 5/1 = 5.0
- 2/5 = 0.4
- 7/10 = 0.7
Exemplos de números racionais negativos:
- -1/3 = -0.333…
- -2/5 = -0.4
- -7/2 = -3.5
- -11/4 = -2.75
- -5/1 = -5.0
Conversão de fração para decimal e vice-versa: Para converter uma fração em decimal, divide-se o numerador pelo denominador. Para converter um decimal finito em fração, escreve-se o decimal como uma fração com denominador 10 n, onde n é o número de casas decimais, e simplifica-se a fração. Decimais periódicos requerem um método ligeiramente diferente, envolvendo equações.
Dez exemplos de números racionais:
- 3
- -5
- 2/3
- -4/7
- 0.6
- -0.25
- 0
- 1.333…
- -2.75
- 100
Exemplos de Números Irracionais
Números irracionais são caracterizados por suas representações decimais infinitas e não periódicas. Alguns exemplos notáveis incluem π, e e raízes quadradas de números não quadrados perfeitos.
Cinco exemplos de números irracionais:
- √2: A raiz quadrada de 2 não pode ser expressa como uma fração de inteiros. Sua representação decimal é infinita e não periódica (aproximadamente 1.41421356…).
- π (pi): A razão entre a circunferência de um círculo e seu diâmetro, aproximadamente 3.14159265359… Sua irracionalidade foi provada matematicamente.
- e (número de Euler): A base dos logaritmos naturais, aproximadamente 2.718281828459… Sua irracionalidade também foi provada.
- √5: A raiz quadrada de 5 é um número irracional, com uma representação decimal infinita e não periódica (aproximadamente 2.236067977…).
- √7: Similarmente à √5 e √2, a raiz quadrada de 7 é irracional, com expansão decimal infinita e não periódica.
π e e são irracionais porque suas representações decimais são infinitas e não apresentam padrão de repetição.
Um número irracional é identificado por sua representação decimal infinita e não periódica. A ausência de um padrão repetitivo na sequência de dígitos após a vírgula é a característica definidora.
| Número Irracional | Aproximação Decimal |
|---|---|
| √2 | 1.41421356… |
| π | 3.14159265359… |
| e | 2.718281828459… |
| √5 | 2.236067977… |
| √7 | 2.645751311… |
Representação Decimal de Números Racionais e Irracionais
A representação decimal é uma ferramenta crucial para diferenciar números racionais de irracionais. A diferença reside na natureza finita ou infinita e periódica ou não periódica de suas expansões decimais.
Números racionais possuem representações decimais finitas (como 0.25) ou periódicas (como 0.333…). Números irracionais, por outro lado, sempre possuem representações decimais infinitas e não periódicas.
Por exemplo, 1/4 = 0.25 (decimal finito), enquanto 1/3 = 0.333… (decimal periódico). Em contraste, π = 3.1415926535… e √2 = 1.41421356… são exemplos de decimais infinitos e não periódicos, característicos de números irracionais.
Operações com Números Racionais e Irracionais, De Um Exemplo De Numero Racional E Um De Iracional

As operações aritméticas fundamentais (adição, subtração, multiplicação e divisão) são realizadas de maneira diferente para números racionais e irracionais.
Operações com números racionais: A adição, subtração, multiplicação e divisão de números racionais resultam sempre em um número racional (exceto a divisão por zero). As operações são realizadas de acordo com as regras usuais da aritmética.
Operações com números irracionais: Operações com números irracionais podem levar a resultados racionais ou irracionais. Por exemplo, √2
– √2 = 2 (racional), mas √2 + √3 é irracional. A imprecisão inerente à representação decimal de números irracionais pode introduzir erros de arredondamento em cálculos.
As propriedades das operações com números racionais são bem definidas e fechadas, enquanto as operações com irracionais podem apresentar resultados menos previsíveis, frequentemente necessitando de aproximações.
Os números racionais e irracionais são densos na reta real, o que significa que entre quaisquer dois números reais, existe um número racional e um número irracional.

