O Que É Um Numero Natural Exemplo – O Que É Um Número Natural? Vamos mergulhar no fascinante mundo dos números naturais, explorando sua definição, propriedades, usos e representações, enquanto desvendamos sua rica história.
Números naturais são os blocos de construção fundamentais da matemática, servindo como base para operações aritméticas e conceitos avançados. Compreender sua essência é crucial para desvendar os mistérios do universo numérico.
Definição de Número Natural
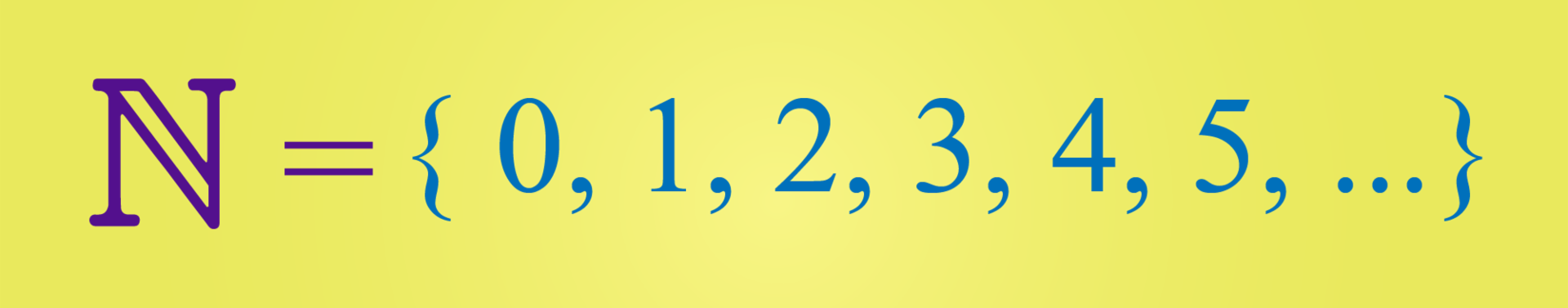
Os números naturais são os números usados para contar, como 1, 2, 3, 4 e assim por diante. Eles são usados para representar quantidades discretas e são fundamentais para a matemática.
Os números naturais têm as seguintes propriedades:
- Eles são todos positivos.
- Cada número natural tem um sucessor, que é o próximo número na sequência.
- Não há um número natural maior que todos os outros números naturais.
Os números naturais são usados em muitas aplicações diferentes, como:
- Contar objetos
- Medir quantidades
- Resolver problemas
Os números naturais são um conceito fundamental na matemática e são usados em muitos campos diferentes.
Propriedades dos Números Naturais

Os números naturais possuem diversas propriedades algébricas, de ordenação, aditivas e multiplicativas que os tornam fundamentais para a compreensão e utilização em diversas áreas da matemática.
Propriedades Algébricas
As propriedades algébricas dos números naturais incluem:
- Comutatividade:A ordem dos números em uma operação não altera o resultado. Por exemplo, 3 + 5 = 5 + 3.
- Associatividade:A forma de agrupamento dos números em uma operação não altera o resultado. Por exemplo, (3 + 5) + 7 = 3 + (5 + 7).
- Distributividade:A multiplicação distribui-se sobre a adição. Por exemplo, 3 × (5 + 7) = 3 × 5 + 3 × 7.
- Elemento neutro:O número 1 é o elemento neutro da multiplicação, pois qualquer número multiplicado por 1 resulta no próprio número. Por exemplo, 3 × 1 = 3.
- Elemento inverso:Todo número natural possui um elemento inverso para a multiplicação, que é o próprio número. Por exemplo, o elemento inverso de 3 é 1/3.
Propriedades de Ordenação
Os números naturais possuem propriedades de ordenação que permitem compará-los e ordená-los:
- Menor que:O símbolo “<" indica que um número é menor que outro. Por exemplo, 3 < 5.
- Maior que:O símbolo “>” indica que um número é maior que outro. Por exemplo, 5 > 3.
- Igual a:O símbolo “=” indica que dois números são iguais. Por exemplo, 3 = 3.
- Transitividade:Se a< b e b < c, então a < c.
- Princípio da boa ordenação:Todo subconjunto não vazio de números naturais possui um menor elemento.
Propriedades Aditivas e Multiplicativas
Os números naturais também possuem propriedades aditivas e multiplicativas:
- Associatividade da adição:A ordem de soma dos números não altera o resultado. Por exemplo, (3 + 5) + 7 = 3 + (5 + 7).
- Comutatividade da adição:A ordem dos números na adição não altera o resultado. Por exemplo, 3 + 5 = 5 + 3.
- Propriedade da identidade aditiva:O número 0 é o elemento neutro da adição, pois qualquer número somado a 0 resulta no próprio número. Por exemplo, 3 + 0 = 3.
- Associatividade da multiplicação:A ordem de multiplicação dos números não altera o resultado. Por exemplo, (3 × 5) × 7 = 3 × (5 × 7).
- Comutatividade da multiplicação:A ordem dos números na multiplicação não altera o resultado. Por exemplo, 3 × 5 = 5 × 3.
- Propriedade da identidade multiplicativa:O número 1 é o elemento neutro da multiplicação, pois qualquer número multiplicado por 1 resulta no próprio número. Por exemplo, 3 × 1 = 3.
Usos dos Números Naturais

Os números naturais têm uma ampla gama de aplicações práticas e teóricas. Eles são usados para quantificar, medir e modelar aspectos do mundo real.
Na vida cotidiana, os números naturais são usados para:
- Contar objetos (por exemplo, frutas, pessoas, carros)
- Medir quantidades (por exemplo, comprimento, peso, volume)
- Indicar ordem (por exemplo, primeiro, segundo, terceiro)
Matemática, O Que É Um Numero Natural Exemplo
Em matemática, os números naturais são usados em várias áreas, incluindo:
- Teoria dos números:Estuda as propriedades dos números naturais, como divisibilidade e números primos.
- Álgebra:Usados em equações, funções e outras estruturas algébricas.
Outras Disciplinas
Além da matemática, os números naturais também são usados em outras disciplinas, como:
- Física:Para descrever quantidades físicas, como energia, velocidade e massa.
- Ciências da Computação:Para representar dados, indexar arrays e controlar loops.
Representações dos Números Naturais
Os números naturais podem ser representados de diversas maneiras, cada uma com suas vantagens e aplicações específicas.
Sistema Decimal
O sistema decimal é o mais comum e utilizado em nosso dia a dia. Ele é baseado no número 10, ou seja, cada posição representa uma potência de 10. Por exemplo, o número 123 representa 1 centena (10²), 2 dezenas (10¹) e 3 unidades (10⁰).
Sistema Binário
O sistema binário é amplamente utilizado em computação e eletrônica. Ele é baseado no número 2, ou seja, cada posição representa uma potência de 2. Por exemplo, o número 1101 representa 1 unidade (2³), 1 dezena (2²) e 0 centenas (2¹).
Tabela de Representações
A tabela a seguir mostra alguns números naturais representados em diferentes sistemas:
| Número Natural | Sistema Decimal | Sistema Binário | Sistema Hexadecimal |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 10 | 10 | 1010 | A |
| 100 | 100 | 1100100 | 64 |
| 1000 | 1000 | 1111101000 | 3E8 |
Símbolos e Notação
Existem vários símbolos e notações usados para representar números naturais:
- Algarismos arábicos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
- Algarismos romanos (I, V, X, L, C, D, M)
- Notação científica (por exemplo, 1,23 x 10³)
- Símbolo de infinito (∞)
História dos Números Naturais: O Que É Um Numero Natural Exemplo

Os números naturais são os blocos de construção fundamentais da matemática, e sua história remonta aos primórdios da civilização humana. O desenvolvimento dos números naturais foi um processo gradual, com diferentes civilizações contribuindo para o nosso entendimento atual.
As Civilizações Antigas e os Números Naturais
As primeiras civilizações, como os sumérios e os egípcios, desenvolveram sistemas numéricos para contar e registrar objetos. Esses sistemas eram baseados em agrupamentos de objetos, como conchas ou grãos, e eram usados principalmente para fins práticos, como comércio e tributação.
Os babilônios desenvolveram um sistema numérico avançado que incluía o conceito de zero e o uso de um sistema posicional, onde o valor de um número dependia de sua posição no número.
Os Gregos e os Números Naturais
Os gregos antigos fizeram contribuições significativas para a teoria dos números naturais. Pitágoras e seus seguidores acreditavam que os números eram a base de todas as coisas e desenvolveram teorias sobre as propriedades dos números naturais, incluindo números primos e números perfeitos.
Euclides, em seus “Elementos”, forneceu uma definição formal de números naturais e estabeleceu as bases para a teoria dos números.
Os Indianos e os Números Naturais
Os matemáticos indianos fizeram avanços significativos na teoria dos números naturais. Eles desenvolveram o sistema numérico decimal, incluindo o uso do zero, e inventaram símbolos para representar números.
Aryabhata, um matemático indiano do século V, introduziu o conceito de números negativos e desenvolveu métodos para resolver equações.
Os Árabes e os Números Naturais
Os matemáticos árabes preservaram e ampliaram o conhecimento dos números naturais desenvolvido pelas civilizações anteriores. Eles introduziram o sistema numérico indo-arábico, que usamos hoje, e fizeram contribuições significativas para a teoria dos números.
Al-Khwarizmi, um matemático árabe do século IX, desenvolveu métodos para resolver equações lineares e quadráticas e introduziu o conceito de álgebra.
Cronograma de Marcos Importantes
- c. 3000 a.C.: Os sumérios desenvolvem um sistema numérico baseado em agrupamentos de objetos.
- c. 1900 a.C.: Os babilônios desenvolvem um sistema numérico posicional que inclui o conceito de zero.
- c. 500 a.C.: Pitágoras desenvolve teorias sobre as propriedades dos números naturais.
- c. 300 a.C.: Euclides fornece uma definição formal de números naturais em seus “Elementos”.
- c. 500 d.C.: Aryabhata introduz o conceito de números negativos e desenvolve métodos para resolver equações.
- c. 800 d.C.: Os matemáticos árabes introduzem o sistema numérico indo-arábico.
- c. 900 d.C.: Al-Khwarizmi desenvolve métodos para resolver equações lineares e quadráticas e introduz o conceito de álgebra.
Nosso mergulho nos números naturais revelou sua natureza fundamental, propriedades intrigantes e aplicações práticas. Eles são a espinha dorsal da matemática, permitindo-nos quantificar, medir e entender o mundo ao nosso redor. Sua história milenar é um testemunho de sua importância inabalável, moldando nosso pensamento e avançando nosso conhecimento.
FAQ Explained
O que são números naturais?
Números naturais são os números usados para contar: 1, 2, 3, 4, 5…
Quais são as propriedades dos números naturais?
Números naturais são fechados sob adição e multiplicação, são bem ordenados e possuem outras propriedades algébricas e de ordenação.
Onde os números naturais são usados?
Números naturais são usados na contagem, medição, matemática, física, ciências da computação e outras disciplinas.

